随机平滑是一种流行的ML防御方法，用于训练可证明稳健的模型，并验证模型对特定输入数据点的鲁棒性。其核心原理是通过采样高斯噪声来探索数据点周围的区域，从而证明模型在对抗样本攻击下的稳健性。本文展示了一种全新的攻击，攻击者利用随机平滑机制中的随机性进行后门攻击，仅需进行极小的更改即可实现攻击且难以被检测。通过在随机数生成器中植入隐藏攻击，传统的 NIST 随机性测试无法检测到这种异常。

0x01 简介

随机性在机器学习（ML）中至关重要，并在多个领域有着广泛的应用。首先，在联邦学习（Federated Learning）中，随机性有助于确保参与者的多样性并防止偏见的产生。其次，随机性被广泛用于优化方法，是随机梯度下降算法（SGD，Stochastic Gradient Descent）的基础。最后，随机性构成了差分隐私（Differential Privacy）技术的核心，通过向数据中添加噪声来保护个人隐私，同时允许进行准确的统计分析。

很少有人考虑到弱随机性可能带来的安全风险。本文提出了两种针对随机平滑（Randomized Smoothing）的攻击方法，并假设攻击者可以影响模型所依赖的随机数生成器。第一种是简单攻击（Native Attack），即用不同的分布（例如拉普拉斯噪声）替换高斯分布。这种方法会显著破坏高或低置信度的量化。下图直观地展示了这种攻击效果。操纵噪声歪曲了真实的决策空间，导致了不正确的预测置信度。

基于这一简单的概念验证，本文进一步构建了一种更隐蔽的攻击：位翻转伪随机数生成器（Bit-flipping PRNG，Pseudo Random Number Generator）攻击。在这种攻击中，随机数生成器的实现中每 64 位深度仅改变一位。这种方法可能导致真实置信度的量化错误高达 81 倍，并且几乎难以被检测到。

这凸显了当前标准和防御措施在防范针对机器学习随机性攻击方面的不足。因此，这些标准不足以在面对复杂攻击者时，确保机器学习系统的安全性和隐私性。本研究旨在帮助研究人员和从业者深入理解他们对工具链中随机性来源的信任程度，并推动开发更强大的防御措施，以防止这种信任被滥用。

0x02 背景与知识

A. 对抗性样本

对抗样本是机器学习模型在面对特定扰动时的鲁棒性问题。对抗样本通过在输入数据上施加细微但有针对性的扰动，使模型做出错误的预测。攻击者的目标是最小化模型的判别函数，从而生成能够误导模型的输入，并尽可能保持与原始输入的相似性。衡量原始输入与扰动输入之间差异的距离函数通常是特定于应用领域的，并对扰动的最大大小施加限制。深度学习模型极易受到逃避攻击（Evasion Attack）的影响。为了确定给定输入 x^0 的最佳对抗性扰动，攻击者的目标是最小化 L : X -> R，其中 L 是模型的判别函数：

对于距离函数d： X x X -> R 的选择通常是特定于领域的，用于衡量原始输入与扰动输入之间的差异，并对扰动的大小施加限制dmax。

B. 随机平滑

随机平滑是一种用于提高机器学习模型（特别是深度神经网络）在对抗性攻击下鲁棒性的方法。它通过随机性为输入添加噪声，生成多个邻近点的预测，从而构造一个更加平滑和稳健的分类器。其核心思想是将一个可能不鲁棒的分类器 f 转化为一个新的分类器 g，使得后者的鲁棒性得到显著提高。其过程包括以下步骤:

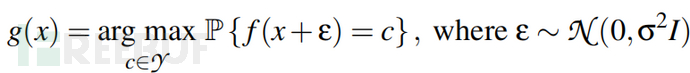
输入加噪：给定一个输入样本 x，对它添加高斯噪声 ε，生成多个扰动样本 x + ε。

多数投票：对于每个生成的扰动样本，利用原始分类器 f 进行预测。统计原始分类器对扰动样本的预测结果，选择出现次数最多的类别作为最终分类结果。

概率框架：新的分类器 g 的预测结果可以理解为 g(x)，P 表示分类器 f 在加入噪声后的预测分布。

随机平滑方法可以证明其鲁棒性边界。例如，对于高斯噪声，如果加入的噪声强度足够高，分类器 g 在输入扰动范围内的预测结果是稳定的。随机平滑的方法不需要直接修改模型结构或重新训练，而是通过对输入添加噪声和多数投票构造出新的鲁棒分类器。随机平滑为鲁棒性提供了可验证的理论边界。例如，基于高斯噪声的随机平滑可以严格保证分类器的预测在一定 l2 范围内保持不变。

读者可以把随机平滑类比为在绘画时用模糊工具将图像边缘平滑化。如果你直接在边缘上修改图像，可能会导致图像质量下降。而通过模糊工具（加入噪声），使边缘更鲁棒，即使稍微修改图像，整体效果依然不受影响。

C. 对抗攻击中的随机性

在对抗性机器学习领域，随机性在攻击和防御中扮演着重要角色。对抗性样本的生成过程常常从随机初始化中受益，而许多机器学习系统工程师主张通过基于随机预处理的防御方法，例如在推理阶段对输入进行随机变换。目前已知有两种攻击依赖于操控随机性：批量重新排序攻击（Batch Reordering Attack）和随机增强攻击（Randomised Augmentation Attack）。前者通过操控数据顺序实施攻击，而后者通过操控增强过程中的随机性，将后门引入目标模型。

D. 随机数生成器

尽管可以从多种分布中进行抽样来生成随机序列，但在计算机编程中，通常使用均匀分布 U(a,b)，即在区间 a 到 b 之间，每个数字被选中的概率相同。标准均匀分布可以转换为任何其他随机分布，因此它是随机数生成器（RNG，Random Number Generator）的自然起点。计算机可以利用多种熵源来生成随机数，例如击键时间或鼠标移动等。

一个依赖键盘击键时间作为熵源的 RNG 可以被建模为一个实验，描述为“两个击键之间的时间（以毫秒为单位）是否为偶数？” 这个实验的结果要么是 0，要么是 1，从而生成一个随机位。对于每次随机实验，将其结果映射为实数值的函数被称为随机变量。随机变量是数学模型中用于描述随机过程的重要工具，用于表示随机实验的不同结果。一维随机变量X在实线上的分布函数可以定义为：

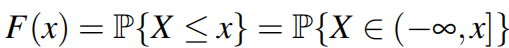
在计算机诞生之初，人们投入了大量研究精力来开发生成随机数的有效方法。当时，有一些机械设备被用来生成随机数，例如 ERNIE，它被用于生成投资彩票的随机数，并可能连接到计算机上。如今，现代 CPU 通常配备了内置的硬件RNG，这些 RNG 利用电流中微小的自然波动来生成随机位。

然而，20 世纪 50 年代机械 RNG 所面临的局限性同样适用于这些现代硬件 RNG。首先，硬件 RNG 很难重现随机程序的输出，从而无法轻松检查程序是否按预期运行。此外，硬件 RNG 可能以程序难以检测到的方式发生故障，导致生成的随机数存在异常。另一个问题是，很难基于现实世界的属性来准确判断 RNG 的熵水平。最后，一个特别值得关注的问题是，确定硬件 RNG 的分布函数非常困难，因为这一分布函数可能受到系统设计者无法控制的环境因素的影响。

这些问题促使伪随机数生成器（PRNG）的发展。PRNG 依赖确定性计算来生成看似随机但实际上是可预测的数字序列。1946 年，冯·诺依曼提出了第一个 PRNG，即中间平方（middle-square）。PRNG 通过序列中的当前数字或计数器来生成下一个数字，但它们需要一个初始值——种子（seed）——来生成第一个数字或计数器值。因此，生成的数字序列是种子的函数。如果种子相同，则同一 PRNG 的不同实例将生成相同的序列。

E. 线性同余法和 PCG64

目前最流行的随机数生成器使用线性同余法，该方法将生成一个数字序列 X1、X2...，如下所示：

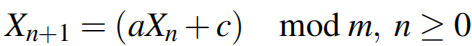
其中 m 为模量，决定了生成数的范围；a 为乘法器；c 为增量；X0 为初始种子。该公式用于生成 0 到 m 之间的随机数。不同的 a 和 c 选择会显著影响生成器的性能和

4A评测 - 免责申明

本站提供的一切软件、教程和内容信息仅限用于学习和研究目的。

不得将上述内容用于商业或者非法用途，否则一切后果请用户自负。

本站信息来自网络，版权争议与本站无关。您必须在下载后的24个小时之内，从您的电脑或手机中彻底删除上述内容。

如果您喜欢该程序，请支持正版，购买注册，得到更好的正版服务。如有侵权请邮件与我们联系处理。敬请谅解！

程序来源网络，不确保不包含木马病毒等危险内容，请在确保安全的情况下或使用虚拟机使用。

侵权违规投诉邮箱：4ablog168#gmail.com（#换成@）